Step 5: Green’s Functions#
Features
Triangular cells
pylith.meshio.MeshIOPetsc
pylith.problems.TimeDependent
pylith.materials.Elasticity
pylith.materials.IsotropicLinearElasticity
pylith.faults.FaultCohesiveKin
pylith.faults.KinSrcStep
field split preconditioner
Schur complement preconditioner
pylith.bc.DirichletTimeDependent
spatialdata.spatialdb.UniformDB
pylith.meshio.OutputSolnBoundary
pylith.meshio.DataWriterHDF5
“Green’s functions”
Fault slip impulses
Simulation parameters#
In this example we compute static Green’s functions for fault slip and use then in Step 6 to invert for fault slip. We generated the “observations” for the slip inversion in Step 4.
We impose fault slip impulses over the central portion of the strike-slip fault (-25 km \(\le\) y \(\le\) +25km), which is slightly larger than where we specified coseismic in Step 4. Fig. 64 summarizes the boundary conditions and fault slip.
The parameters specific to this example are in step05_greensfns.cfg.
Fig. 64 Boundary conditions for static Green’s functions. We set the x and y displacement to zero on the +x and -x boundaries and prescribe left-lateral slip impulses.#
We use the GreensFns problem and specify the fault on which to impose fault slip impulses.
As in Step 4, we include output at the fake GPS stations using OutputSolnPoints.
In the fault interfaces section we set the fault type to FaultCohesiveImpulses for our fault where we want to impose fault slip impulses for the Green’s functions.
We also use a spatial database to limit the section of the fault where we impose the fault slip impulses to -25 km \(\le\) y \(\le\) +25 km.
Important
Currently, a basis order of 1 (default) for the slip auxiliary subfield is the only choice that gives accurate results in a slip inversion due to the factors described here.
The basis order for the slip auxiliary subfield controls the representation of the slip field for the impulses. For a given impulse, a basis order of 1 will impose unit slip at a vertex with zero slip at all other vertices. Likewise, a basis order of 0 will attempt to impose unit slip over a cell with zero slip in all other cells; however, this creates a jump in slip at the cell boundaries that cannot be accurately represented by the finite-element solution. As a result, you should not use a basis order of 0 for the slip auxiliary field. A basis order of 2 will impose slip at vertices as well as edge degrees of freedom in the cell. Because PyLith output decimates the basis order to 0 or 1, you should avoid this choice of basis order as well until we provide better ways to output fields discretized with higher order basis functions.
[pylithapp]
problem = pylith.problems.GreensFns
[pylithapp.greensfns]
label = fault
label_value = 20
[pylithapp.problem.interfaces]
fault = pylith.faults.FaultCohesiveImpulses
[pylithapp.problem.interfaces.fault]
impulse_dof = [1]
db_auxiliary_field = spatialdata.spatialdb.SimpleDB
db_auxiliary_field.description = Fault rupture auxiliary field spatial database
db_auxiliary_field.iohandler.filename = slip_impulses.spatialdb
auxiliary_subfields.slip.basis_order = 1
Running the simulation#
$ pylith step05_greensfns.cfg
# The output should look something like the following.
>> /software/unix/py39-venv/pylith-debug/lib/python3.9/site-packages/pylith/meshio/MeshIOObj.py:44:read
-- meshiopetsc(info)
-- Reading finite-element mesh
>> /src/cig/pylith/libsrc/pylith/meshio/MeshIO.cc:94:void pylith::meshio::MeshIO::read(topology::Mesh *)
-- meshiopetsc(inf
-- Component 'reader': Domain bounding box:
(-50000, 50000)
(-75000, 75000)
# -- many lines omitted --
-- Component 'problem': Computing Green's function 12 of 12.
0 SNES Function norm 3.027654014252e-03
Linear solve converged due to CONVERGED_ATOL iterations 46
1 SNES Function norm 2.204080482014e-12
Nonlinear solve converged due to CONVERGED_ITS iterations 1
>> /software/unix/py39-venv/pylith-debug/lib/python3.9/site-packages/pylith/problems/Problem.py:201:finalize
-- greensfns(info)
-- Finalizing problem.
WARNING! There are options you set that were not used!
WARNING! could be spelling mistake, etc!
There are 3 unused database options. They are:
Option left: name:-ts_error_if_step_fails (no value)
Option left: name:-ts_monitor (no value)
Option left: name:-ts_type value: beuler
The beginning of the output written to the terminal matches that in our previous simulations.
The second half of the output written to the terminal resembles the output from time-dependent problems, but with the time step information replaced by the impulse information.
The journal info associated with the GreensFns component (journal.info.greensfns) turns on the impulse information.
We get warnings about unused PETSc options because we do not use time stepping.
Visualizing the results#
The output directory contains the simulation output.
Each “observer” writes its own set of files, so the solution over the domain is in one set of files, the boundary condition information is in another set of files, and the material information is in yet another set of files.
The HDF5 (.h5) files contain the mesh geometry and topology information along with the solution fields.
The Xdmf (.xmf) files contain metadata that allow visualization tools like ParaView to know where to find the information in the HDF5 files.
To visualize the data using ParaView or Visit, load the Xdmf files.
In Fig. 65 we use ParaView to visualize the y displacement field using the viz/plot_dispwarp.py Python script.
As in Step 4 we override the default name of the simulation file with the name of the current simulation.
>>> SIM = "step05_greensfns"
Next we run both the viz/plot_dispwarp.py and viz/plot_dispstations.py Python scripts as described in ParaView Python Scripts.
Tip
You can use the “play” button (right triangle) to flip between the solution for the different fault slip impulses.
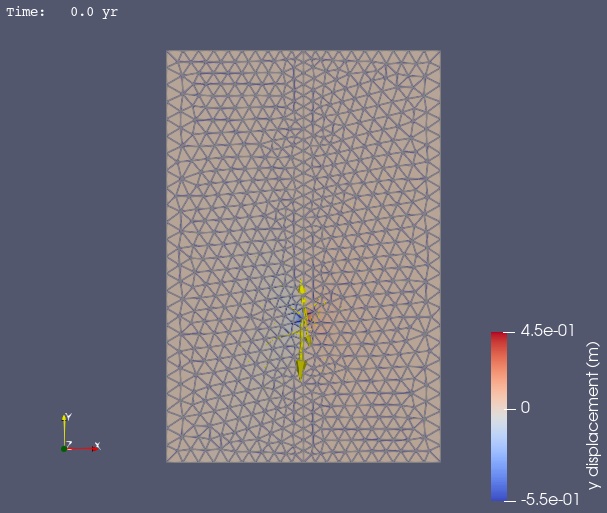
Fig. 65 Solution for Step 4. The colors of the shaded surface indicate the magnitude of the y displacement, and the deformation is exaggerated by a factor of 1000. The displacement vectors at the fake GPS stations use en exaggeration factor of 50,000.#

